今回は令和1年(2019年)法規の問13を解いていきます。
テブナンの定理が出てきました。完全にやり方を忘れていました。。。
他にも解き方があると思います!!

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋
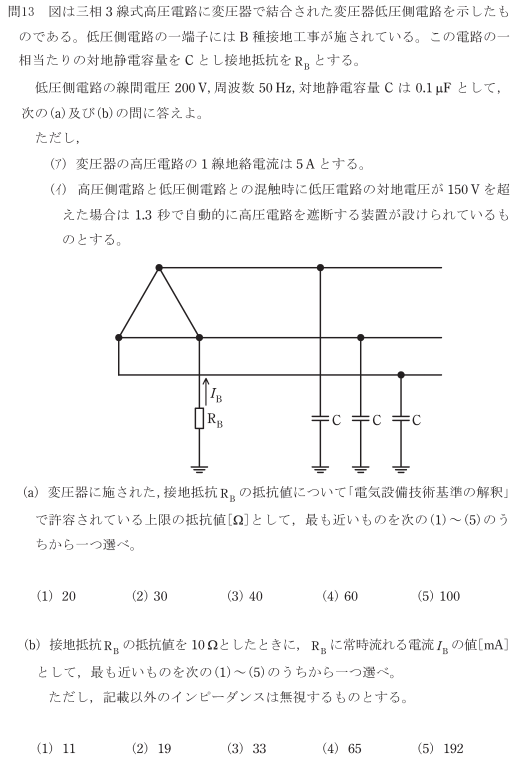
(a)解答
・線間電圧200V
・遮断時間1.3秒
なので、
\(\displaystyle R_B=\frac{300}{I_g}\)
です
\(I_g=5A\)

\(I_g=5A\)なので
\(\displaystyle R_B=\frac{300}{I_g}=\frac{300}{5A}=60Ω\)
ですね!!
正解(4)60Ω
(b)解答
これは理解に苦しみました
まだまだ理解度が低いなーと思いました
テブナンの定理とかあんまり使わないし!!
ってことで解いていきます。

電流\(I_B\)を求めたいのでテブナンの定理を使っていきます(覚えたて)
テブナンの定理
\(\displaystyle I=\frac{V_{ab}}{R_0+R}\)
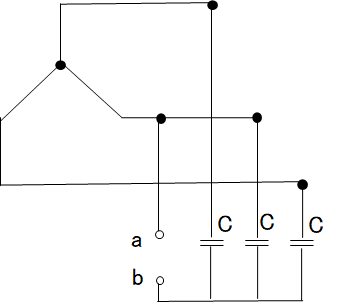
電流を求めたいところの抵抗\(R_B\)を取り除きます。

次に\(V_{ab}\)の電圧を求めていきます。
このままだとわからないので、Δ→Yに変換します
・線間電圧は200Vなので相電圧は\(\displaystyle \frac{200}{\sqrt{3}}V\)
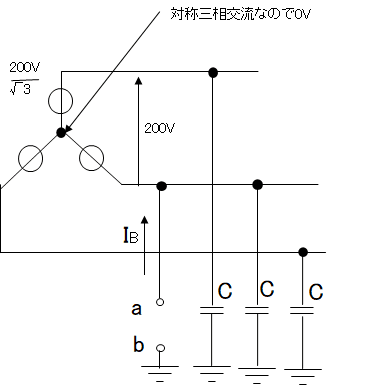
必要な部分だけ抜き出してみました。
\(V_{ab}\)は\(\displaystyle \frac{200}{\sqrt{3}}V\)となりますね!

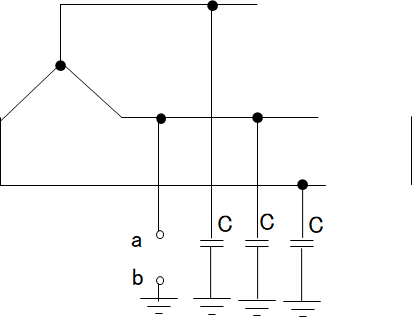
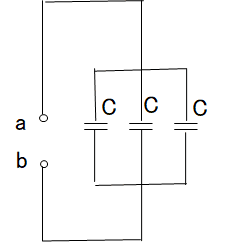
次に回路の合成抵抗\(\dot{R_0}\)を求めます。
テブナンの定理では電圧源はすべて短絡して合成抵抗を求めます
最終的に合成抵抗\(\dot{R_0}\)は3Cです
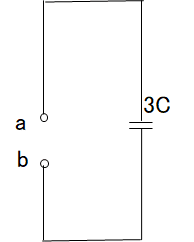
コンデンサの並列は足し算でOK!!
テブナンの式に代入していきます
テブナンの定理
\(\displaystyle \dot{I_B}=\frac{\dot{V_{ab}}}{\dot{R_0}+\dot{R_B}}\)
\(\displaystyle =\frac{V_{ab}}{\frac{1}{j3\omega C}+R_B}\)
\(\omega=2\pi f\)
\(\displaystyle =\frac{V_{ab}}{\frac{1}{j6\pi fC}+R_B}\)
\(I_B\)を大きさに変換(三平方の定理)
\(\displaystyle =\frac{V_{ab}}{\sqrt{(\frac{1}{6\pi fC})^2+(R_B)^2}}\)
数字を代入して
\(\displaystyle =\frac{\frac{200}{\sqrt{3}}}{\sqrt{(\frac{1}{6 \times \pi \times 50 \times 0.1\times 10^{-6}})^2+(10)^2}}A\)
\(=10.88 \times 10^{-3}A\)
\(=10.88 mA\)
正解(1)11A

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋



コメント